Memenuhi Tugas Softskill (Desain Permodelan Grafik) Semester 5 (2015/2016)
Pembahasan : Cubehelix Diagram
Mata Kuliah : Desain Permodelan Grafik
Mata Kuliah : Desain Permodelan Grafik
Kata Pengantar
Puji dan syukur kehadirat tuhan yang maha Esa atas segala rahmat dan taufik nya, dan tidak lupa juga kepada rekan kelompok 3 penyusunan buku ini sehingga kami dapat menyelesaikan penyusunan buku ini dengan judul Cubehelix Diagram. Kami harap buku ini dapat dipergunakan sebagai pengetahuan, wawasan, dan petunjuk untuk orang banyak.
Harapan kami semoga buku ini dapat membantu dan memberi wawasan yang lebih luas tentang Cubehelix dan pewarnaan dengan menggunakan software yang akan dibahas. Buku ini kami akui masih banyak kekurangan karena pengalaman yang kami miliki sangat kurang. Oleh kerena itu kami harapkan kepada para pembaca untuk memberikan masukan-masukan yang bersifat membangun untuk kesempurnaan makalah ini. Terima kasih kepada rekan rekan kelompok dalam pengerjaan penulisan ini, berkat bantuannya dan semangat dalam penulisan ini, buku ini telah selesai dengan baik, dan terima kasih untuk Dr. rer. Nat. I Made Wiryana, Skom, SSI, MAppScc telah memberikan kesempatan dalam menyelesai kan penulisan dengan konsep yang di berikan, semoga menjadi bermanfaat.
Depok, 1 Februari 2016
Penyusun
Bab 1
Pendahuluan
1.1 Latar Belakang
Abad ini adalah abad dimana teknologi berkembang pesat, semua bidang yang ada di dunia ini sudah berlomba-lomba menciptakan teknologi yang paling baru dan belum pernah diciptakan sebelumnya. Mulai dari Pertanian, Industri, Otomotif, Pendidikan, dan tak ketinggalan dengan dunia kedokteran dan bidang-bidang lainnya. Cubehelix diciptakan untuk membantu banyak sekali bidang, misalnya pada bidang kesehatan cubehelix digunakan untuk membantu orang-orang yang mengidap buta warna, dalam bidang kenegaraan cubehelix digunakan untuk pemetaan kependudukan negara dengan cara menstatistikan bagian-bagian wilayah, dan pada bidang geografis digunakan untuk menentukan kontur-kontur seperti pegunungan, tanah dan lain-lain. Cubehelix di ciptakan dengan berbagai kegunanannya di berbagai bidang dengan menggunakan degradasi warna yang ada di dalamnya.
CubeHelix adalah skema warna yang jenuh yang diperoleh dari warna hitam dan putih . Itu tidak selalu dari warna yang palet dan paling artistik, tetapi cubehelix memiliki keuntungan untuk menjadi lebih mudah melihat bagi orang-orang dengan buta warna . Dengan mengubah berbagai pengaturan , banyak variasi pada ” CubeHelix ” skema yang mungkin terjadi .
1.2 Rumusan Masalah
Setelah uraian diatas dapat dirumuskan masalah sebagai berikut.
1. Apa definisi dari Cubehelix ?
2. Apa Kegunaan dari Cubehelix?
3. Bagaimana Implementasi dan Pemanfaatan Cubehelix ?
1.3 Tujuan Penulisan
Berdasarkan rumusan masalah yang telah di kemukakan diatas, maka tujuan di tulisnya buku ini adalah membahas Cubehelix, apa kegunaan dari cubehelix, bagaimana dan apa software untuk menggunakan cubehelix . Diharapkan dengan di tulisnya buku ini pembaca dapat memberi pengetahuan tentang Cubehelix .
Bab 2
Konsep
2.1 Definisi Cubehelix
Cubehelix adalah skema warna yang digunakan untuk menampilkan gambar Intensitas Astronomi. Skema ini digunakan untuk meningkat kontras cahaya saat greyscale dicetak dalam dua buah warna yaitu hitam dan putih. Cubehelix sendiri tidak memiliki persepsi mendasar mengenai peningkatan kecerahan warna yang digunakan, misalnya warna merah untuk nilai data yang tinggi, dan untuk nilai data menengah digunakan warna kuning atau hijau, untuk mengganti cahaya terang dari warna merah. Untuk mengevaluasi fungsi helix, helix bergerak melalui pemodelan warna yaitu RGB “kubus”, mulai dari hitam (0,0,0) dan berakhir pada warna putih (1,1,1). Poin merata pada helix dalam kubus dikembalikan sebagai warna RGB, Ini memberikan pallet warna yang intensitasnya meningkat secara monoton, yang merupakan pentransfer yang baik untuk menampilkan grayscale atau cetakan. Serta dapat memiliki keuntungan bagi penderita warna blindeness(buta warna). Banyaknya skema warna yang digunakan untuk menampilkan gambar intensitas astronomi tidak memiliki peningkatan yang mendasari terkait persepsi kecerahan warna yang digunakan. Warna adalah properti visual yang sering semua orang gunakan dalam suatu visualisasi tanpa mereka sadari hal itu. Contohnya pada variasi color map pelangi sangat populer, namun terkadang dapat bermasalah dan menyesatkan. Peta warna pelangi tersebut didasarkan pada warna dalam spektrum cahaya, kadangkala peta warna dalam urutan benar, dan kadangkala juga peta warna dalam urutan yang salah. Kecepatan warna pelangi itu merupakan salah satu yang akan menjadi masalah. Bahkan jika warna tersebut digunakan secara konsisten, tak seorang pun akan tahu urutan yang tepat. Sehingga Nama-nama warna mempengaruhi persepsi kita tentang warna. Dibawah ini merupakah bagian bagian warna dengan perhitungannya.
• Putih (0,0-0,09). Putih merupakan bagian warna yang masih belum tercampur dengan apapun dan putih adalah warna yang digunakan untuk memulai
• Merah muda (0,1-0,19 dan 0,2-0,29).
• Ungu (0,3-0,39). Merupakan warna yang lebih gelap dari warna merah.
• Biru (0,4-0,49 dan 0,5-0,59). Merupakan warna yang berbeda juga tentunya dengan yang lain, dan warna yang berlawanan dari warna pink.
• Hijau (0,6-0,69 dan 0,7-0,79). Warna yang hampir mendekati dari warna biru, namun warna hijaun jauh lebih cerah dari warna biru.
• Kuning kehijauan (0,8-0,89). Warna kuning kehijauan memiliki rona warna yang jauh lebih cerah dari warna hijau dan hampir mendekati warna kuning.
• Kuning (0,9-0,99). Warna kuning ini adalah warna asli, sehingga jika warna lain seperti warna biru dicampurkan dengan warna kuning sehingga menghasilkan warna kuning.
• Oranye dan coklat (1.0 dan lebih dari 1.0). Warna oranye dan cokelat memang hampir mendekati namun warna oranye jauh lebih cerah daripada warna cokelat.
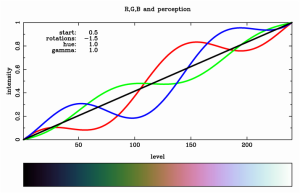
Seperti yang dikemukakan Dave Green (2011) Skema contoh ‘ Cubehelix ‘ memiliki warna dengan 256 tingkat warna , dan baru-baru ini ditambahkan dalam CASA . Variasi dalam intensitas merah, hijau dan biru , dan intensitas yang dirasakan sesuai dengan persamaan
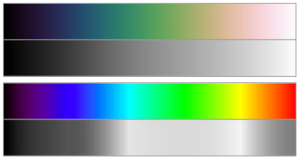
1. Bawah : baji warna untuk menggambarkan skema . Ini memiliki warna awal 0,5 , yaitu ungu (antara R = 1 dan B = 3 ≡ 0 bila menggunakan modulo 3 aritmatika , dengan R = 1 , G = 2 , B = 3 ) , dengan -1,5 rotasi , yaitu → B → G → R → B , nilai hue 1,2 ( seperti dengan warna awal dipilih dan rotasi nilai ini tidak menyebabkan setiap kliping ) , dan gamma dari 1,0 .
kisaran 0-1 , colour scheme dimulai pada ( R , G , B ) = ( 0,0,0 ) , yaitu hitam , dan berakhir di ( R , G , B ) = ( 1,1,1 ) , yaitu putih . Untuk beberapa fraksi λ antara 0 dan 1 , warna abu-abu adalah warna yang sesuai pada nilai fraksi sepanjang hitam menjadi putih diagonal , yaitu ( λ , λ , λ ) , ditambah elemen warna . Itu elemen warna dihitung dalam pesawat intensitas yang dirasakan konstan, yang dapat didefinisikan dalam hal dua Unit ( R , G , B ) vektor warna ( -0,074 , -0.146,0.986 ) dan ( 0,891 , -0.453,0.0 ) , yang pertama yang didominasi warna biru . Unsur warna tambahan dari skema dikendalikan oleh tiga parameter .
• Awal warna ( s ) . Ini adalah arah penyimpangan warna dominan hitam dari pada awal skema warna .
• Jumlah R , G , B rotasi ( r ) dalam warna yang dibuat dari awal (yaitu hitam ) ke end (yaitu putih ) dari skema warna .
• Parameter rona (h ) , mengontrol warna yang jenuh . Amplitudo colourdeviation dari greydiagonal adalah nol di setiap akhir dan terbesar di tengah. Jika parameter ini adalah nol maka skema warna adalah murni greyscale dan meningkatkan kecerahan . Jika parameteris terlalu besar , maka R , G , B mungkin keluar dari 0-1 berbagai dekat awal atau akhir skema warna , sehingga harus terpotong ( meskipun jika hanya beberapa tingkat warna yang terpotong , skema warna yang dihasilkan , mungkin masih memuaskan ) .
Cubehelix merupakan satu-satunya colorscheme-generator yang dibutuhkan. Cubehelix colormaps terbaik untuk dokumen yang diterbitkan atau didistribusikan. Pengajuan tersebut memungkinkan kita untuk membuat colormaps berbeda menggunakan beberapa parameter. Standar algoritma Cubehelix menawarkan colorschemes sangat menarik untuk dokumen online dan elektronik, akan tetapi bila dicetak di grayscale informasi tetap pada urutan data yang asli. Informasi tersebut juga mencakup dua kontrol tambahan atas jangkauan dan domain dari skema Cubehelix, memberikan sejumlah praktis tak terbatas dari colormaps dengan gaya yang berbeda, dengan skema maksimal yang berbeda, multi ataupun warna tunggal cocok untuk pencetakan grayscale atau bahkan grayscale sederhana. Sehingga mencakup tiga fungsi untuk bekerja dengan Cubehelix colormaps:
• “Cubehelix” mengembalikan colormap yang dibuat menggunakan Cubehelix fungsi colorscheme Dave Green.
• “Cubehelix_view” menciptakan angka untuk menciptakan colorschemes Cubehelix dengan real-time penyesuaian interaktif dari nilai parameter skema, ditambah modus demonstrasi ‘acak’ dan kemampuan untuk mengendalikan tokoh lainnya ‘atau sumbu’ colormaps.
• “Cubehelix_find” dapat digunakan untuk mengambil parameter dari Cubehelix colormap yang ada, atau menemukan yang terbaik Cubehelix colorscheme yang cocok setiap pilihan warna (misalnya dokumen atau colorscheme perusahaan).
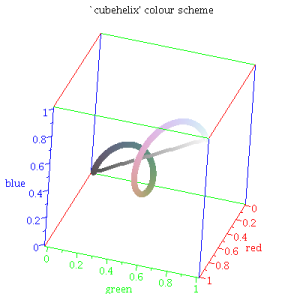
Cubehelix Colorschemes terdiri dari node helix yang panjang dan meruncing dalam warna RGB, dengan terus meningkatnya intensitas yang dirasakan (hitam > putih). Sehingga skema yang mendefinisikan colormaps menarik dengan pilihan hue, saturasi dan kecerahan, dan belum mencetak angka (atau gambar) pada warna hitam dan putih (misalnya postscript) hasil dalam grayscale monoton akan terus meningkat dalam mempertahankan urutan kecerahan aslinya pada colormaps tersebut. Urutan informasi colormap dipertahankan bahkan didalam grayscale, yang berarti gambar dengan warna menarik dapat dicetak dalam grayscale dan masih informatif kepada pengguna akhir. Fitur yang paling penting dalam cubehelix adalah mencetak dengan baik dalam menggunakan warna hitam dan putih. Karena hal tersebut dapat menghemat waktu yang besar ketika membuat angka untuk publikasi dimana warna yang hanya tersedia secara online (seperti di Astronomi yang masih menggunakan jurnal dengan salinan cetak).
Cubehelix ini dapat diselesaikan dengan melalui kubus RGB, sambil terus meningkatkan saturasi (hitam putih). Angka unik tersebutlah, yang menjelaskan bagaimana cubehelix bekerja. Cubehelix juga memiliki informasi dengan hasil yang lebih padat. Ketik menggunakan warna untuk peta kontur, kita mencoba untuk menyampaikan dimensi ketiga data pada ruang 2D.
Dengan warna pelangi, kita dapat mengandalkan warnanya. Dengan cubehelix kita dapat melakukan hal tersebut dengan baik, yaitu warna dan saturasi seperti yang akan kita inginkan, bahkan secara efektif kita dapat melakukannya untuk beberapa dataset sekaligus.
Ketika Cubehelix dapat melakukan saturasi dengan benar, maka banyak orang yang mencetak dengan printer hitam putih akan menyukainya. Cubehelix dapat mencetak kontur yang menakjubkan dengan memetakan kontur dengan cara yang benar. Hal Ini berlaku secara ganda untuk menampilkan angka pada proyektor. Jika saluran pada proyektor yang berwarna merah padam, atau kuning lemah, plot kita akan menjadi antipeluru. Jika kita berpikir tentang warna dengan degradasi yang aneh di visualisasi data kita, kita tidak berpikir tentang hasil wawasan atau groundbreaking yang dapat mencoba untuk menunjukkannya. Namun cubehelix cukup ramah untuk pembaca yang mengalami penyakit buta warna.
Cubehelix umumnya kurang begitu baik untuk semua bentuk penyakit buta warna, karena perubahan konstan dalam warna yang jenuh. Sekitar 8-10% pria memiliki bentuk kekurangan persepsi tentang warna, dan jika kita membuat peta kerapatan warna dengan pelangi normal yang jenuh, maka sama saja kita mengubah warna tersebut sehingga warnanya berubah menjadi abstrak.
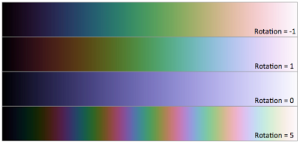
Cubehelix memiliki beberapa kegunaan seperti tombol yang dapat kita sesuaikan. Hal ini termasuk kedalam beberapa warna pelangi, lalu dari warna apa untuk memulainya, arah mana saja yang harus dilalui, seberapa cepat untuk menuju warna dari warna hitam ke warna putih, dan bagaimana warna jenuh untuk membuat warna. Beberapa contoh sederhana untuk menunjukkan fleksibilitas. Di bawah ini merupakan bebrapa tes untuk menunjukkannya:
1. Skema default dibuat mundur melalui roda pelangi sebanyak sekali (rotasi = -1, vibgyor),
2. setelah melalui roda arah yang tepat,
3. Gerakan nol warna (hanya hitam ke putih) kemudian mulai dengan warna biru,
4. Dan setelah itu coba 5 kali melalui warna pelangi.
Hal tersebut akan berlangsung dari hitam menjadi putih, menyimpang jauh dari abu-abu murni (yaitu diagonal dari hitam menjadi putih dalam kubus warna) menggunakan helix meruncing di kubus warna, sambil memastikan terus meningkatnya intensitas yang dirasakan. Deviasi dari diagonal memperhitungkan bahwa merah, hijau dan biru tidak dianggap sama dalam hal intensitas. Skema warna Ini kemudian dicetakan sebagai greyscale perangkat postscript hitam dan putih.
Persamaan yang menciptakan skema warna yang ditetapkan untuk warna RGB yang sederhana adalah untuk mengkonversi ke kode HEX . Disini ada 5 versi , menggunakan pengaturan yang sering dikerjakan . Sekali lagi , semua dari 100 % hitam sampai dengan 100% putih , dan untuk hitam dan putih .
Berikut adalah 5 skema CubeHelix , dengan # 1 menjadi ” standar ” palet :
2.2 Penggunaan Cubehelix Pada Pewarnaan
Mode Warna (Color mode) adalah cara representatif warna pada aplikasi grafis yang berdasarkan pada model warna. Sedangkan model warna yang ada saat ini adalah RGB (Red, Green, Blue), CMYK (Cyan, Magenta, Yellow, dan Black), HSV (Hue, Saturation, Value), Lab, Bitmap, Grayscale, Duptone, Indexed, dan Mutichannel. Dalam dunia komputer grafis, dikenal beberapa macam model warna yang masing-masing model warna memiliki keunggulan, kekuragan, dan karakteristik sendiri-sendiri.
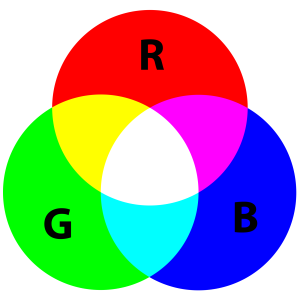
2.2.1 Mode Warna RGB
Ketika Anda menggunakan aplikasi grafis, dalam palet Channel akan mendapati tiga buah channel tunggak yaitu channel Red, Green, dan Blue. Sedangkan sebuah channel lainnya adalah RGB. Sebetulnya channel RGB bukanlah merupakan channel melainkan channel preview kombinasi ketiga channel yang lainnya. Masing-masing channel berisi informasi warna. Masing-masing warna dalam mode ini memiliki 256 tingkat gradasi, hal ini dapat dibuktikan dengan melihat angka maksimal dari nilai masing-masing warna tersebut pada kotak dialog Color Picker. Bila diperhatikan, warna merah (Red) memiliki nilai skala 0 hingga 255 yang berarti jumlah keseluruhan tingkat gradasinya ada 256. 256 sama dengan 2 8 . Hal ini mengandung arti satu channel berisi informasi warna 8 bit, dan oleh karena terdapat tiga channel maka berarti keseluruhan warna RGB menyimpan informasi 24 bit. Meskipun begitu, bukan berarti RGB bernilai 8 bit. Itu semua bergantung pada media yang digunakan. Pada film dan kamera digital tingkat bit depth yang mampu ditampilkan RGB bisa mencapai 30 bit, 36 bit atau bahkan lebih dari itu. Dan seperti kita ketahui bahwa bit depth merupakan banyaknya variasi warna yang dapat ditampilkan oleh suatu sistem representasi warna. Jadi bila satu channel bernilai 8 bit artinya channel tersebut menyimpan variasi warna sejumlah 2 8 yaitu 256.
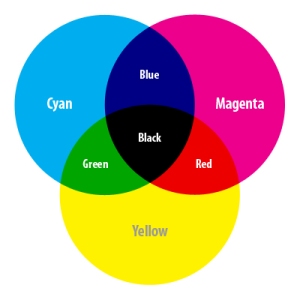
2.2.2 MODE WARNA CMYK
Dalam software disain grafis, ketika membuka palet Channel maka akan nampak empat buah channel tunggal dan satu buah channel preview. Channel tunggal yang dimaksud adalah channel Cyan, Magenta, Yellow, dan Black. Sedangkan channel preview merupakan kombinasi channel Cyan, Magenta, Yellow dan Black sehingga channel tunggal tersebut memiliki nama CMYK.
Nilai maksimal persentase tiap warna adalah 100%, ini bisa dibuktikan dalam kotak dialog Color Picker. Nilai persentase tersebut merupakan nilai persentase tiap warna dalam tinta cetak. Untuk mencetak warna grayscale atau hitam saja maka film yang diperlukan hanya satu yaitu Black. Sedangkan jika ingin mencetak sebuah gambar dengan warna full color maka film yang diperlukan maksimal empat yaitu Cyan, Magenta, Yellow, dan Black. Namun, saat ini sudah terdapat sistem cetak yang menggunakan enam warna atau biasa disebut Hexachrome. Film yang digunakan untuk mencetak dalam sistem Hexachrome ada enam yaitu: Cyan, Magenta, Yellow, Blak, Green, dan Orange.
Model CMYK dilandaskan pada cahaya yang diserap dan kualitas tinta yang dicetakan pada kertas. Cahaya Putih diibaratkan sebagai tinta transparan, dianggap gelombang cahaya yang visible seluruhnya terserap dan yang selainnya direfleksikan kembali menuju mata. Beralih pada sudut pandang tinta, karena setiap tinta yang dicetakan tidak memiliki kemurnian atau intensitas maksimal dari setiap warna , maka ketiga tinta tersebut hanya mampu menghasilkan warna coklat gelap. Untuk menghasilkan warna hitam maka perlu dikombinasikan dengan tinta yang berwarna hitam. Kombinasi dari seluruh warna tinta printer ini dalam menghasilkan warna terkenal dengan four-color process printing.
2.2.3 MODE WARNA LAB
Apabila Anda menggunakan mode warna Lab, maka pada palet Channel akan nampak tiga buah channel tunggal dan satu buah channel preview. Channel tunggal tersebut adalah channel Lightness/Luminance, channel a, dan channel b. Channel a dan b menyimpan informasi komponen kromatik. Channel a menyimpan informasi kromatik dari hijau hingga merah sedangkan channel b menyimpan informasi kromatik dari biru hingga kuning. Nilai skala untuk Lightness/Luminance berkisar 0 sampai 100 sedangkan nilai kromatik a dan b berkisar -120 sampai dengan 120.
L*a*b color model merupakan pemodelan warna yang diproposalkan oleh Commission Internationale d’Eclairage (CIE) pada 1931 sebagai as an standar internasional bagi ukuran warna. pada 1976, model ini telah dirapihkan dan diberi nama CIE L*a*b.
L*a*b color didesain sebagai ukuran yang tidak dipengaruhi oleh device, sehingga pembentukannya tidak terpengaruh dari sudut pandang device yang terkait dengannya (seperti monitor, printer, computer, ataupun scanner) sebagai pembentuk output misalkan image.
L*a*b color terdiri dari luminance atau lightness component (L) dan dua chromatic components: a component (from green to red) dan b component (from blue to yellow)
2.2.4 MODE WARNA BITMAP
Apabila Anda menggunakan mode warna Bitmap, maka mode warna ini hanya menyimpan informasi 1 bit. Dengan kata lain, mode warna ini hanya menyimpan informasi dua warna saja. Warna yang akan ditampilkan adalah warna hitam dan putih. Jadi ketika Anda mengkonfersi gambar ke dalam mode warna ini maka warna yang terang (dekat dengan putih) akan berubah menjadi putih sedangkan warna yang mendekati hitam akan berubah menjadi hitam. Mode warna ini berguna untuk membuat halftone screen pada saat akan mencetak gambar tersebut (umumnya untuk sablon). Resolusi gambar serta jenis dan tekstur halftone screen dapat diatur sesuai kebutuhan.
2.2.5 MODE WARNA GRAYSCALE
Mode warna ini menyimpan informasi bit depth warna sebesar 8 bit. Jadi warna yang bisa ditampilkan pada mode warna grayscale berjumlah sampai 256. Skala perhitungan numeriknya bisa dengan pendekatan nilai brightness yang berskala 0 sampai 255 atau dapat pula menggunakan pendekatan persentase tinta hitam yang memiliki skala 0 sampai 100%.
Berikut sekilas panduan untuk mengkonversi image menuju dan dari mode Grayscale:
Kita dapat mengkonversikan baik dalam bentuk Bitmap-mode dan image berwarna kedalam mode grayscale.
Untuk mengkonversikan image berwarna ke dalam bentuk image grayscale dengan kualtas yang baik, adapun pemberian level dari keabuan (shades) dari piksel hasil konversi merupakan hasil representasi ulang level kecerahan (luminosity) dari gambar asli.
2.2.6 MODE WARNA DUOTONE
Mode warna ini biasa digunakan untuk mendapatkan gambar dengan dua warna. Duotone memiliki arti duo tone atau dua warna. Pada saat menggunakan mode warna duotone, gambar yang dibuat hanya menggunakan dua channel warna saja. Anda dapat menentukan sendiri warna yang diinginkan. Selain mode warna duotone, tersedia pula mode warna monotone, tritone, dan quadtone. Monotobe berarti satu warna, Tritone berarti tiga warna, dan Quadtone berarti empat warna.
2.2.7 MODE WARNA INDEXED
Mode warna ini biasa digunakan untuk keperluan electric web publishing (web, animasi, dan multimedia). Hal ini disebabkan karena pada mode warna ini akan dikompres menjadi hanya 256 warna atau dalam jumlah yang Anda inginkan sehingga ukuran file menjadi kecil (mengalami penyusutan). Ketika mengkonversi gambar dari mode warna lain ke mode warna Indexed maka Adobe Photoshop akan membuat CLUT (Color Look Up Table). CLUT berisi beberapa warna yang dominan pada gambar Anda dan berjumlah sampai 256. Warna yang ke 257 dan seterusnya akan digabungkan ke warna yang terdekat yang masuk dalam daftar 256 warna.
2.2.8 MODE WARNA MULTICHANNEL
Mode warna ini digunakan untuk menguraikan informasi duotone, tritone, dan quadtone sebelum dicetak menjadi channel-channel tunggal. Selain itu, ketika membuang satu channel atau lebih pada mode warna RGB, CMY maupun CIE Lab maka secara otomatis mode warna akan berubah menjadi multichannel. Pada contoh di bawah ini bermula dari mode warna RGB kemudian diubah menjadi mode warna Multichannel maka informasi channel akan berubah.
2.3 Menggunakan Kustom Warna Palet
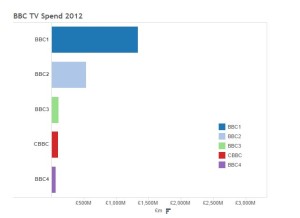
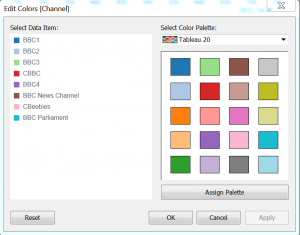
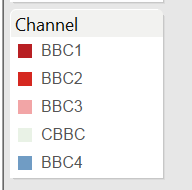
Disini terdapat contoh yaitu menggunakan Tableau, Tableau memiliki kemampuan untuk menciptakan warna dengan menggunakan RGB . Dengan menggunakan ini Anda dapat menyesuaikan grafik dan dashboard untuk mencocokkan pedoman disini sebagai contoh adalah perusahaan BBC. Grafik di bawah ini menunjukkan 5 saluran top BBC dengan pengeluaran pada tahun 2012. Hal ini menggunakan default Tableau Warna Palet
Untuk mengubah warna di Tableau Desktop Anda dapat klik dua kali warna pada legenda warna itu sendiri . Maka muncul standar pilih menu warna . Jika Anda klik dua kali pada kotak biru di sebelah kategori , BBC 1 dalam contoh ini , Anda dapat menyesuaikan warna dengan memilih warna yang berbeda , mengubah gradien atau dengan menentukan kode RGB .
Ini bekerja dengan baik untuk satu grafik , namun itu akan menjadi tugas yang sulit jika dilakukan pada setiap visualisasi dibangun di setiap perusahaan . Sementara itu Tableau tidak memungkinkan untuk penciptaan palet warna kustom tambahan . Untuk melakukan ini, Anda perlu mengubah file Preferences.tps yang dapat ditemukan di ‘ My Tableau Repository Folder ‘ . Repositori secara default ditemukan dalam folder My Documents pada komputer pengguna Tableau Desktop . Arahkan ke Repositori dan klik kanan pada file preferensi . Anda dapat membuka file di Notepad atau editor teks lainnya .
File menggunakan format xml standar. Untuk menambahkan palet warna Anda dapat menggunakan sintaks berikut
<preferences>
<color-palette name=”BBC Colour Scheme” type=”regular” >
<color>#B81F1E</color>
</color-palette>
</preferences>
Setiap warna harus dimasukkan dalam bagian ‘ Warna – palet’ . Tidak seperti di dalam Deskto harus menggunakan HTML Hex Kode . Setiap kode harus diawali dengan #. Setelah memasukkan masing-masing warna Anda dapat menyimpan file preferensi . Anda perlu menutup dan membuka kembali Tableau untuk preferensi baru untuk memuat . Sekarang jika mengedit warna maka akan melihat palet warna baru yang tercantum dalam dropdown dengan warna yang Anda baru saja ditetapkan .
File preferensi perlu diinstal pada semua mesin lokal bagi pengguna untuk dapat menggunakan palet selama desain . Warna-warna akan tetap muncul pada visualisasi jika dimuat di komputer lain tetapi palet tidak akan tersedia . Microsoft Paint memungkinkan kita untuk mendapatkan RGB untuk setiap pixel pada gambar. Dan memuat atau menyisipkan gambar di MS Paint dan menggunakan pemetik Warna (terlihat seperti penetes mata ) untuk memilih pixel dan kemudian pilih ‘Edit warna ‘ yang tepat paling pada toolbar untuk mengungkapkan kode RGB untuk warna yang dipilih .
2.4 Psikologi Warna
Warna adalah spektrum tertentu yang terdapat di dalam suatu cahaya sempurna (berwarna putih). Identitas suatu warna ditentukan panjang gelombang cahaya tersebut. Sebagai contoh warna biru memiliki panjang gelombang 460 nanometer. Panjang gelombang warna yang masih bisa ditangkap mata manusia berkisar antara 380- 780 nanometer.
Dalam peralatan optis, warna bisa pula berarti interpretasi otak terhadap campuran tiga warna dasar: merah, hijau, biru yang digabungkan dalam komposisi tertentu. Misalnya pencampuran 100% merah, 0% hijau, dan 100% biru akan menghasilkan interpretasi warna magenta. Dalam seni rupa, warna bisa berarti pantulan tertentu dari cahaya yang dipengaruhi oleh pigmen yang terdapat di permukaan benda. Misalnya pencampuran pigmen magenta dan cyan dengan proporsi tepat dan disinari cahaya putih sempurna akan menghasilkan sensasi mirip warna merah. Setiap warna mampu memberikan kesan dan identitas tertentu sesuai kondisi sosial pengamatnya. Misalnya warna putih akan memberi kesan suci dan dingin di daerah Barat karena berasosiasi dengan salju. Sementara di kebanyakan negara Timur warna putih memberi kesan kematian dan sangat menakutkan karena berasosiasi dengan kain kafan (meskipun secara teoritis sebenarnya putih bukanlah warna). Di dalam ilmu warna, hitam dianggap sebagai ketidakhadiran seluruh jenis gelombang warna. Sementara putih dianggap sebagai representasi kehadiran seluruh gelombang warna dengan proporsi seimbang.
2.5 Warna dan Device
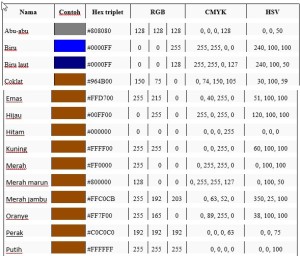
Setiap Device memiliki keterbatasan, begitupun dengan device penghasil output warna (contohnya: monitor, scaner, printer). Tidak seluruh warna dalam spektrum visible dapat didisplaykan oleh device penghasil output warna. Berikut adalah daftar beberapa warna yang dapat didisplaykan device pada umumnya disertai nilai parameter sesuai pemodelannya
Tabel 1. Daftar Warna
Makna Warna
Abu-abu
Elegan, rendah hati, hormat, kemuliaan, stabilitas, kepelikan, tidak terbatas waktu, kebijakan
Anakhronisme(penempatan kejadian pada waktu yang salah), bosan, jemu, pudar, kelemahan, bodoh, debu, polusi, gelandangan
Merah
hasrat, kuat, energi, api, cinta, seks, kegembiraan, kecepatan, panas, kepemimpinan, maskulin, tenaga
Bahaya, api, Danger, fire, tanpa rasa, darah, perang, marah, revolusi, radikal, agresi, berhenti
Biru
Laut, langit, damai, kesatuan, harmoni, Seas, skies, peace, unity, harmony, ketenangan, sentosa, kesejukan, percaya diri, air, es, loyalitas, konservatif, , dapat diandalkan, dapat dipercaya, teknologi, musim dingin, kebersihan
Depresi, dingin, idealisme, Depression, cabul, es, musim dingin
Hijau
Alam, musim semi, kesuburan, kemudaan, lingkungan ,sejahtera, uang (AS), semoga berhasil, enerjik, pergi, rumput, dermawan
Agresi, tidak berpengalaman, iri hati, kemalangan, cemburu, uang, sakit, kikir
Kuning
Cahaya matahari, kesenangan, kegembiraan, optimisme, idealisme, kemakmuran (emas), musim panas, harapan, udara.
Pengecut, pesakitan (karantina) resiko, tidak jujur, tamak, kelemahan, kewanita-wanitaan
Ungu Sensualitas, spiritual, kreativitas, kemakmuran, keluarga raja, bangasawan, upacara, misteri, kebijakan, pencerahan
Arogan, flamboyan, kemurungan, tanpa rasa, sumpah serapah, melebih- lebihkan, kebingungan
Oranye Budisme, energi, keseimbangan, panas, api, antusias, flamboyan, suka bermain
Agresi, arogan, flamboyan, tanpa rasam peringatan, bahaya, api, danger, fire
Putih Penghormatan, kesucian, salju, damai, murni, bersihm aman, rendah hati, pernikahan, penyeterilan, musim dingin ,
Kedinginan, penyetirilan, rumah sakit, menyerah, ketakutan, pengecut, musim dingin, tidak imajinatif
Berbagai budaya melihat warna secara berbeda. Di India, biru diasosiasikan dengan Krisna (berasosiasi sangat positif), hijau dengan Islam, merah dengan kemurnian (digunakan dalam warna pernikahan) dan coklat dengan kesedihan. Dalam kebanyakan budaya Asia, kuning adalah warna imperial dengan asosiasi budaya yang serupa terhadap warna ungu dalam dunia barat. Di Cina, merah merupakan simbol perayaan, keberuntungan dan kemakmuran, putih disimbolkan dengan kesedihan dan kematian, sementara hijau topi berarti seorang istri berbuat selingkuh. Di Eropa warna sangat kuat diasosiasikan dengan partai politik dibandingkan di Amerika. Di banyak negara, hitam disinonimkan dengan sifat konservatif, merah dengan sosialisme, sementara coklat sering langsung diasosiasikan dengan Nazi. Banyak orang percaya bahwa biru adalah warna terbaik karena paling banyak memiliki nilai positif dan paling kecil nilai negatif dalam asosiasi budaya di berbagai ragam budaya.
Studi menunjukkan kebanyakan warna memiliki lebih banyak asosiasi positif daripada negatif, dan meskipun ketika sebuah warna memiliki asosiasi negatif, secara umum hanya digunakan pada konteks tertentu.
2.6 Efek Warna dalam Desain
– Bentuk dulu baru warna
– pastikan bentuk dikenali lebih dahulu sebelum ditambahkan warna
– Gubakan warna yang senada untuk membuat hubungan antara produk dengan pesan yang disampaikan
– Gunakan untuk hubungan antara produk dengan logo
– Gunakan warna untuk membuat hierarki informasi
– Jangan gunakan drop shadows kecuali memang diperlukan (hanya menekankan produk/judul)
– Seimbangkan antara image dengan teks
2.7 Cubehelix Colormap untuk Python
Kami menggunakan Python untuk penelitian kami ,dalam 2 tahun terakhir perpustakaan dan dokumentasi untuk hal-hal astronomi Python telah mencapai ” massa kritis ” , dan membuat transisi untuk banyak hal belum pernah lebih mudah !. Namun, satu masalah kecil khususnya Matplotlib : warna dalam angka biasanya mengerikan.
Matplotlib sudah memiliki colormap cubehelix standar telah dibangun, serta beberapa colormaps yang sangat baik dan desaturate . Apa yang membuat algoritma cubehelix begitu kuat adalah bahwa hal yang mendefinisikan keluarga colormaps bahwa semua desaturate adalah benar . Ini adalah apa yang hilang saat di Matplotlib .
Komunitas Python memiliki sikap yang kuat ” memasang atau tutup mulut ” , jadi saya menghabiskan beberapa jam menerjemahkan pelaksanaan IDL saya cubehelix ke Python !
berikut adalah sintak untuk colormap dalam python
import numpy as np
import matplotlib.pyplot as plt
import cubehelix
# set up some simple data to plot
x = np.random.randn(10000)
y = np.random.randn(10000)
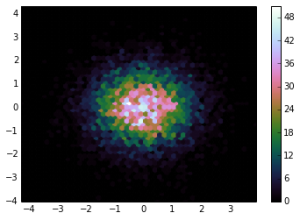
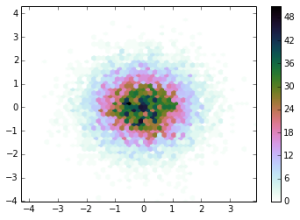
# create the default “cubehelix” colormap
cx1 = cubehelix.cmap()
plt.hexbin(x,y,gridsize=50,cmap=cx1)
plt.colorbar()
plt.show()
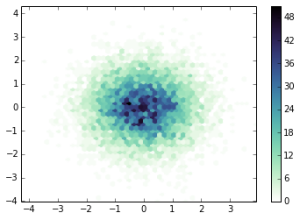
# Reverse of the default “cubehelix” colormap
# I think this is more appropriate for density maps,
# as intensity corresponds with density.
cx2 = cubehelix.cmap(reverse=True)
plt.hexbin(x,y,gridsize=50,cmap=cx2)
plt.colorbar()
plt.show()
# My favorite flavor of “cubehelix”,
# mostly blue with a small hue change
cx3 = cubehelix.cmap(reverse=True, start=0.3, rot=-0.5)
plt.hexbin(x,y,gridsize=50,cmap=cx3)
plt.colorbar()
plt.show()
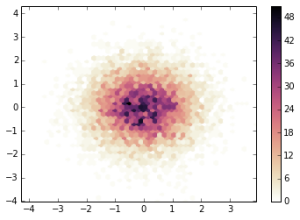
# Another good version, mostly using red/purples
cx4 = cubehelix.cmap(reverse=True, start=0., rot=0.5)
plt.hexbin(x,y,gridsize=50,cmap=cx4)
plt.colorbar()
plt.show()
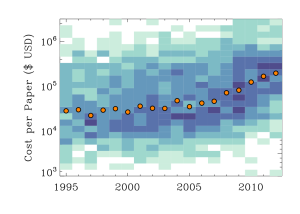
CUBEHELIX sudah termasuk dalam versi matplotlib. Jika Para astronom menggunakan IDL untuk merencanakan sesuatu , saya telah membuat untuk menggunakan versi tersebut dengan mudah . Beberapa versi lain ada juga , misalnya situs web Dave Green untuk rincian . Jika lingkungan bahasa pilihan tidak termasuk , disana dapat membuat palet warna kustom menggunakan vektor RGB ( atau mungkin bahkan dengan kode hex ) hampir sepele untuk kode up skema warna asli seperti yang kami lakukan di IDL ( menggunakan kertas asli ) .
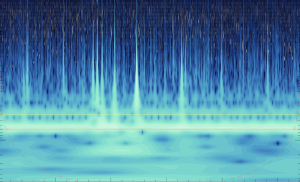
Akhirnya , berikut adalah beberapa contoh menyenangkan yang kami dapat, dan menggunakan berbagai pengaturan CUBEHELIX.
Bab 3
Implementasi Software Cubehelix
3.1 Software untuk Cubehelix
Cubehelix adalah skema warna yang di gunakan untuk menampilkan gambar intensitas Astronomi, yang sifatnya monoton atau hanya dapat meningkatkan kecerahan saat di tampilkan di greyscale (hitam putih). Biasanya Cubehelix digunakan sebagai alat pembantu bagi penderita buta warna, pemetaan Negara dan kependudukan, menentukan kontur, dan degradasi warna.
Software yang di gunakan biasanya berbentuk scientific plotting. Sebuah teknik grafis untuk mewakili satu set data, biasanya sebagai grafik yang menunjukkan hubungan antara dua variabel atau lebih. Plot dapat di gambar dengan tangan atau oleh plotter mekanik atau elektronik. Grafik adalah representasi visual dari hubungan antara variabel. Grafik juga dapat digunakan untuk membaca nilai variabel yang tidak diketahui diplot. Grafik fungsi dapat digunakan dalam matematika, ilmu pengetahuan, teknik, teknologi, keuangan, dan lain lain. Plot memainkan peran penting dalam statistik dan analisis data. Prosedur di sini dapat secara luas dibagi menjadi dua bagian : kuantitatif dan grafis. Teknik kuantitatif adalah serangkaian prosedur statistik yang menghasilkan keluaran numerik atau tabular. Contoh teknik kuantitatif meliputi :
– Uji hipotesa
– Analisi varian
– Estimasi titik dan Interval
– Kuadrat regresi
Prosedur grafis seperti plot adalah jalan singkat untuk mendapatkan wawasan ke dalam kumpulan data dalam hal asumsi pengujian, pemilihan model, validasi model, pemilihan estimator, identifikasi hubungan, faktor penentuan efek, deteksi outlier. Grafik statistik memberikan wawasan aspek struktur yang mendasari data.
3.2 Matlab
Matlab ialah suatu perangkat yang dibuat oleh Math Work Inc., digunakan untuk analisis tematika, rancangan kendali, identifikasi sistem dan grafik.
MATLAB (Matrix Laboratory) adalah sebuah program untuk analisis dan komputasi numerik dan merupakan suatu bahasa pemrograman matematika lanjutan yang dibentuk dengan dasar pemikiran menggunakan sifat dan bentuk matriks. Pada awalnya, program ini merupakan interface untuk koleksi rutin-rutin numerik dari proyek LINPACK dan EISPACK, dan dikembangkan menggunakan bahasa FORTRAN namun sekarang merupakan produk komersial dari perusahaan Mathworks, Inc. yang dalam perkembangan selanjutnya dikembangkan menggunakan bahasa C++ dan assembler (utamanya untuk fungsi-fungsi dasar MATLAB). MATLAB telah berkembang menjadi sebuah environment pemrograman yang canggih yang berisi fungsi-fungsi built-in untuk melakukan tugas pengolahan sinyal, aljabar linier dan kalkulasi matematis lainnya. MATLAB juga berisi toolbox yang berisi fungsi-fungsi tambahan untuk aplikasi khusus . MATLAB bersifat extensible , dalam arti bahwa seorang pengguna dapat menulis fungsi baru untuk ditambahkan pada library ketika fungsi-fungsi built-in yang tersedia tidak dapat melakukan tugas tertentu. MATLAB (Matrix Laboratory) yang merupakan bahasa pemrograman tingkat tinggi berbasis pada matriks sering digunakan untuk teknik komputasi numerik, yang digunakan untuk menyelesaikan masalah-masalah yang melibatkan operasi matematika elemen, matrik, optimasi, aproksimasi dll. Sehingga Matlab banyak digunakan pada :
– Matematika dan Komputansi
– Pengembangan dan Algoritma
– Pemrograman Modeling, Simulasi, dan Pembuatan Prototipe
– Analisa Data , Eksplorasi dan Visualisasi
– Analisis Numerik dan Statistik
– Pengembangan Aplikasi Teknik
– Grafik
MATLAB memiliki beberapa Toolbox diantaranya :
– Toolbox Control System Merupakan perintah untuk membantu dalam penyelesaianteori teknik sistem kendali.
– Toolbox Signal Processing Merupakan perintah untuk membantu dalam penyelesaian proses sinyal digital.
– Toolbox Optimization Merupakan perintah untuk membantu dalam penyelesaian optimasi fungsi umum non linier dan linier.
3.2.1 Fungsi Toolbox Matlab
3.2.1.1 Toolbox Control System
Pada Toolbox ini akan memberikan algoritma standar industri dan aplikasi untuk sistematis menganalisis, merancang, dan tuning sistem kontrol linier. Disini kita dapat menentukan sistemnya sebagai transfer function, state-space, pole-zero-gain, or frequency-response model. Aplikasi dan fungsi seperti langkah respon plot dan bode plot dapat memvisualisasikan perilaku sistem dalam domain waktu dan domain frekuensi. Anda dapat mengatur parameter kompensator otomatis menggunakan kontroler PID tuning, Bode lingkaran membentuk metode akar lokus, LQR / LQG desain, dan teknik interaktif dan otomatis lainnya. Anda dapat memvalidasi desain Anda dengan memverifikasi waktu naik, overshoot, settling time, keuntungan dan margin fase, dan persyaratan lainnya.
3.2.1.2 Toolbox Signal Processing
Pada Toolbox ini akan memberikan algoritma standar industri dan aplikasi untuk analog dan digital signal processing (DSP). Anda dapat menggunakan toolbox untuk memvisualisasikan sinyal dalam domain waktu dan frekuensi, menghitung FFTs untuk analisis spektral, desain FIR dan IIR filter, dan menerapkan konvolusi, modulasi, resampling, dan teknik pemrosesan sinyal lainnya. Algoritma di toolbox dapat digunakan sebagai dasar untuk mengembangkan algoritma khusus untuk audio dan pengolahan pidato, instrumentasi, dan baseband komunikasi nirkabel.
3.2.1.3 Toolbox Optimization
Toolbox ini akan memberikan algoritma yang banyak digunakan untuk optimasi standar maupun besar. Algoritma ini dapat memecahkan masalah diskrit baik dibatasi dan tidak dibatasi. Optimasi perangkat lunak toolbox ini meliputi fungsi untuk pemrograman linear, pemrograman kuadratik, integer programming biner, optimasi nonlinier, nonlinier kuadrat terkecil, sistem persamaan nonlinier, dan optimasi multiobjective. Dengan menggunakan ini dapat mencari solusi yang optimal, melakukan analisis tradeoff, menyeimbangkan beberapa alternatif desain, dan memasukkan metode optimasi menjadi algoritma dan model.
Matlab merupakan bahasa pemrograman level tinggi yang dikhususkan untuk kebutuhan komputasi teknis, visualisasi dan pemrograman seperti komputasi matematik, analisis data, pengembangan algoritma, simulasi dan pemodelan dan grafik-grafik perhitungan Pada awalnya Matlab dibuat untuk memberikan kemudahan mengakses data matrik pada proyek LINPACK dan EISPACK. Saat ini matlab memiliki ratusan fungsi yang dapat digunakan sebagai problem solver mulai dari simple sampai masalah-masalah yang kompleks dari berbagai disiplin ilmu. Dalam lingkungan perguruan tinggi teknik, Matlab merupakan perangkat standar untuk memperkenalkan dan mengembangkan penyajian materi matematika, rekayasa dan kelimuan. Di industri, MATLAB merupakan perangkat pilihan untuk penelitian dengan produktifitas yang tinggi, pengembangan dan analisanya.
Kegunaan MatLab secara umum adalah sebagai berikut
a. Matematika dan komputasi,
b. Perkembangan algoritma,
c. Pemodelan, simulasi, dan pembuatan prototype,
d. Analisa data, eksplorasi dan visualisasim
e. Pembuatan aplikasi, termasuk pembuatan antaramuka grafis
3.3 Karakteristik MATLAB
– Bahasa pemrogramannya didasarkan pada matriks (baris dan kolom).
– Lambat (dibandingkan dengan Fortran atau C) karena bahasanya langsung diartikan.
– Automatic memory management , misalnya kita tidak harus mendeklarasikan arrays terlebih dahulu.
– Tersusun rapi
– Waktu pengembangannya lebih cepat dibandingkan dengan Fortran atau C.
– Dapat diubah ke bahasa C lewat MATLAB Compiler.
– Tersedia banyak toolbox untuk aplikasi-aplikasi khusus.
3.4 Lingkungan Kerja MATLAB
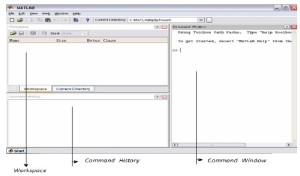
Secara umum lingkungan kerja Matlab terdiri dari tiga bagian yang penting yaitu
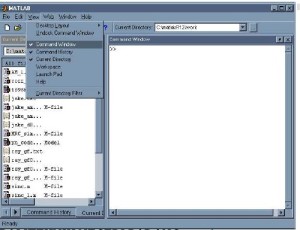
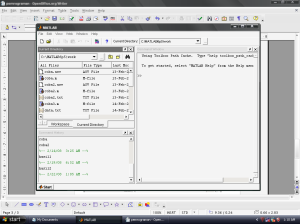
1. Command Windows
Windows ini muncul pertama kali ketika kita menjalankan program Matlab. Command windows digunakan untuk menjalankan perintah-perintah Matlab, memanggil tool Matlab seperti editor, fasilitas help, model simulink, dan lain-lain. Ciri dari windows ini adalah adanya prompt (tanda lebih besar) yang menyatakan Matlab siap menerima perintah. Perintah tersebut dapat berupa fungsi-fungsi bawaan (toolbox) Matlab itu sendiri.
Workspace: Menampilkan semua variable yang pernah dibuat meliputi nama variable, ukuran, jumlah byte dan class.
Command History : Menampilkan perintah-perintah yang telah diketikkan pada command Window
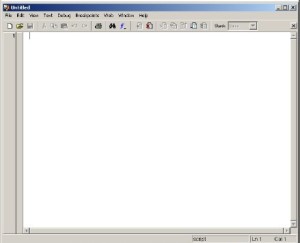
2. Editor Windows
Windows ini merupakan tool yang disediakan oleh Matlab yang berfungsi sebagai editor script Matlab (listing perintah-perintah yang harus dilakukan oleh Matlab). Ada dua cara untuk membuka editor ini, yaitu
1. Klik : File, lalu New dan kemudian M-File
2. Ketik p ada command windows : ”edit”
Secara formal suatu script merupakan suatu file eksternal yang berisi tulisan perintah MatLAb. Tetapi script tersebut bukan merupakan suatu fungsi. Ketika anda menjalankan suatu script, perintah di dalamnya dieksekusi seperti ketika dimasukkan langsung pada MatLAb melalui keyboard. M-file selain dipakai sebagai penamaan file juga bisa dipakai untuk menamakan fungsi, sehingga fungsi fungsi yang kita buat di jendela editor bisa di simpan dengan ektensi .m sama dengan file yang kita panggi dijendela editor. Saat kita menggunakan fungsi Matlab seperti inv, abs, cos, sin dan sqrt, matlab menerima variabel berdasarkan variabel yang kita berikan. Fungsi M-file mirip dengan script file dimana keduanya merupakan file teks dengan ektensi .m
sebagaimana script M-file, fungsi m-file tidak dimasukkan dalam jendela command window tetapi file tersendiri yang dibuat dengan editor teks. Membentuk dan menjalankan M-File:
– Klik menu File , pilih New dan klik M-File
– Pada editor teks, tulis argumen atau perintah
– Simpan dengan cara klik File , pilih Save As dan beri nama dengan ekstensi .m
– Pastikan file yang akan dijalankan berada pada direktori aktif
– Misalkan file graf1.m berada di C:\MATLAB, maka lakukan perintah cd
– >> cd c:\matlab
– Kemudian jalankan file graf1.m dengan cara
– >> graf1
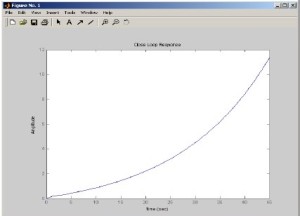
3. Figure Windows
Windows ini merupakan hasil visualisasi dari script Matlab. Matlab memberikan kemudahan bagi programmer untuk mengedit windows ini sekaligus memberikan program khusus untuk itu, sehingga selain berfungsi sebagai visualisasi output yang berupa grafik juga sekaligus menjadi media input yang interaktif
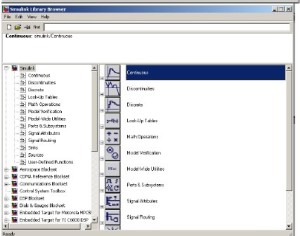
4. Simulink windows
Windows ini umumnya digunakan untuk mensimulasikan system kendali berdasarkan blok diagram yang telah diketahui. Untuk mengoperasikannya ketik “ simulink” pada command windows.
5. Graphics.
MATLAB memiliki fasilitas untuk menampilkan vector dan matrices sebagai suatu grafik. Didalamnya melibatkan high-level functions (fungsi-fungsi level tinggi) untuk visualisasi data dua dimensi dan data tiga dimensi, image processing, animation, dan presentation graphics. Ini juga melibatkan fungsi level rendah yang memungkinkan bagi anda untuk membiasakan diri untuk memunculkan grafik mulai dari bentuk yang sederhana sampai dengan tingkatan graphical user interfaces pada aplikasi MATLAB.
6. MATLAB Application Program Interface (API).
Merupakan suatu library yang memungkinkan program yang telah ditulis dalam bahasa C dan Fortran mampu berinterakasi dengan MATLAB. Ini melibatkan fasilitas untuk pemanggilan routines dari MATLAB (dynamic linking), pemanggilan MATLAB sebagai sebuah computational engine, dan untuk membaca dan menuliskan MAT-files.
MATLAB dibuat dengan mengacu pada bahasa MATLAB, kadang-kadang disebut M-code atau M saja. Cara termudah mengeksekusi (menjalankan) M-code adalah dengan mengetikkannya secara langsung di prompt pada jendela Command Window, sebuah elemen UI di desktop MATLAB. Dengan cara ini, MATLAB dapat digunakan sebagai shell (pengeksekusi perintah) matematis yang interaktif. Urutan-urutan perintah yang lebih kompleks dapat disimpan dan dimasukkan ke dalam sebuah M-file, dengan menggunakan MATLAB Editor, sebagai skrip sehingga dapat memperluas perintah-perintah yang tersedia.
Variabel Variabel didefinisikan dengan operator assignment, =. Perintah pada MATLAB bisa diketik secara dinamis, dalam artian variabel-variabel dapat langsung diisi tanpa mendefinisikan jenisnya terlebih dahulu, kecuali bila variabel tersebut merupakan objek simbolis. Nilai yang diisikan ke sebuah variabel dapat berupa konstan, yang didapat dari hasil perhitungan yang melibatkan variabel lainnya, atau dari keluaran suatu fungsi.
Contohnya:
>> x = 17
x = 17 >>
x = ‘hat’
x = hat
>> x = [3*4, pi/2]
x = 12.0000 1.5708
>> y = 3*sin(x)
y = -1.6097 3.0000
Vektor/Matriks dalam MATLAB
MATLAB adalah sebuah “Matrix Laboratory”, dan karenanya ia menyediakan berbagai cara untuk membuat matriks dengan dimensi berbeda-beda. Menurut gaya bahasa di dalam MATLAB, sebuah vektor mengacu pada sebuah matriks satu dimensi (1×N or N×1), yang biasanya disebut sebagai sebuah array di bahasa pemrograman lainnya. Sebuah matriks umumnya multi-dimensional, yang artinya terdiri dari satu/lebih dimensi, contohnya sebuah matriks N×M, matriks N×M×L, dsb, dimana N, M, and L lebih besar dari 1. Di bahasa lain, matriks seperti ini dapat dilukiskan sebagai array dari array-array, atau array dari array-array dari array-array, atau array multi-dimensi saja.
Untuk membuat array yang sederhana di MATLAB, sintaks penulisan perintahnya adalah nilai awal:langkah:nilai akhir.
Contohnya:
perintah >> array = 1:2:9 array = 1 3 5 7 9 akan membuat sebuah variabel bernama array dengan isi 1, 3, 5, 7 dan 9. Yaitu, sebuah array dengan nilai awal 1, dengan nilai selanjutnya berjarak 2 dari sebelumnya, kemudian berhenti ketika sampai ke 9.
a. Vektor
Baris vektor adalah daftar angka-angka yang dipisahkan oleh koma (,) atau spasi. Jumlah masukan dikenal sebagai panjang vektor. Masukan harus ditulis dalam tanda kurung siku ([]).
b. Matriks
Dapat diasumsikan bahwa didalam MATLAB setiap data akan disimpan dalam bentuk matriks. Dalam membuat suatu data matriks pada MATLAB, setiap isi data harus dimulai dari kurung siku ‘[‘ dan diakhiri dengan kurung siku tutup ‘]’. Untuk membuat variabel dengan data yang terdiri beberapa baris, gunakan tanda ‘titik koma’ (;) untuk memisahkan data tiap barisnya. MATLAB menyediakan beberapa fungsi yang dapat kita gunakan untuk menghasilkan bentuk-bentuk matriks yang diinginkan. Fungsi-fungsi tersebut antara lain: · zeros : untuk membuat matriks yang semua datanya bernilai 0 · ones : matriks yang semua datanya bernilai 1 · rand : matriks dengan data random dengan menggunakan distribusi uniform · randn : matris dengan data random dengan menggunakan distribusi normal · eye : untuk menghasilkan matriks identitas
3.5 GRAFIK
Salah satu keunggulan M ATLAB ialah kemampuannya dalam menampilkan/mengolah grafik dan suara dengan command yang sederhana dan fleksibel. kita akan belajar mengenai visualisasi data (plot grafik 2-dimensi dan 3-dimensi), serta penyuaraan.
Dengan bahasa pemrograman MATLAB, data hasil pengukuran atau hasil analisa dapat divisualisasikan dalam bentuk grafik 2 dimensi atau 3 dimensi. fungsi untuk menggambarkan data dalam bentuk grafik 2Dimensi. yaitu: perintah plot, perintah yang akan memvisualisasikan data perkawanan satu satu antara data pada variabel dependen dengan data pada variabel independen. Bebera fungsi penggambar grafik lainnya yang mirip dengan plot adalah bar dan stairs. MATLAB juga mampu menggambarkan suata data yang berbentuk medan dalam bentuk 2D. Banyak perintah yang dapat digunakan dua diantaranya adalah: menggambar kontur dari medan contour dan menggambar sebaran dari medan pcolor(Z). Praktikum kali ini akan mempelajari cara menggambarkan grafik 2 dimensi dengan MATLAB Integral dengan batas tertentu atau luas daerah dibawah kurva dalam range yang finitive dapat ditentukan dengan tiga buah fungsi yang dimiliki matlab yaitu :
trapz
quad
quad8
fungsi trapz mendekati integral dengan metode trapesium, sedangkan quad berdasar pada metode quadratude. Kebalikan dari integral, diferensial membahas fungsi dalam satu selang yang sangat sempit. Dengan sedikit modifikasi deretan data dapat dideferensial dengan fungsi yang dimiliki MATLAB yaitu polyval dan polyder.
3.6 Dokumentasi Matlab
Matlab memberikan kemudahan bagi para pengguna untuk menemukan bantuan sehubungan dengan semua fasilitas yang diberikan oleh Matlab. Misalnya, bantuan tentang bagaimana memulai Matlab pertama kali, trik pemrograman, membuat grafik 2 dan 3 dimensi, menggunakan tool akuisisi data, pengolahan sinyal, penyelesaian persamaan diferensial parsial.
Untuk memperoleh bantuan tersebut, kita dapat memilih MATLAB Menu dari menu Help. Untuk bantuan tentang Matlab sendiri, dibagi atas beberapa bagian antara lain
– Development Environment, bagian ini akan memberikan informasi yang lengkap mengenai desktop dari Matlab.
– Mathematics, bagian yang menjelaskan bagaimana menggunakan fitur yang dimiliki oleh Matlab untuk dalam mengolah data matematis dan statistik. Isi dalam bantuan ini dicakup antara lain: Matrks dan aljabar linier, polinomial dan interpolasi, analisis data dan statistik, fungsi function, matriks jarang (sparse matrix).
– Programming and data type, bagian ini menjelaskan bagaimana membuat script dan fungsi dengan menggunakan Matlab. Bantuan ini mencakup pemrograman M-File, larik, larik multidimensi, optimalisai performance Matlab, tip pemrograman Matlab.
– Graphics, bagian ini menjelaskan tentang bagaimana membuat atau mengeplot grafik dari data yang kita miliki. Yang termasuk dalam bagian ini antara lain, dasar-dasar pengeplotan, format grafik, membuat grafik khusus misalnya grafik dalam bentuk bar, histogram, contour dan lain-lain
– 3-D Visualization, bagian ini menjelaskan dengan tuntas bagaimana menampilkan data yang kita miliki dalam grafik 3 dimensi, termasuk didalamnya membuat grafik 3D, menentukan tampilan objek, transparansi objek, lighting dan lain-lain
– Creating Graphical User Interfaces, bagian ini menjelaskan bagaimana kita dapat membuat GUI (Graphical User Interface) berbasis Matlab.
Disamping bagian-bagian yang sudah disebutkan di atas, disini juga disertakan beberapa bagian tambahan yang ikut melengkapi dokumentasi penjelasan tentang Matlab, diantaranya function-By cattegory, function-Alphabetical List, handle graphic property browser, external interfaces/API, external interfaces/API references dan lain-lain.
Keterangan
1. tool untuk browse direktori aktif. Dari tool ini kita dapat mengeset direktori mana yang aktif. Direktori aktif berarti bahwa direktori inilah yang siap untuk diakses file didalamnya atau tempat yang siap untuk digunakan sebagai penyimpan data.
2. Tool yang menampilkan direktori aktif. Dari tool ini kita dapat melihat direktori mana yang aktif. Sebagai default direktori aktif Matlab adalah C:\MATLAB6p5\work, jika Matlab diinstal di direktori C:\ , kalau disimpan di D:\ maka direktori aktif defaultnya D:\MATLAB6p5\work, begitu juga di E:\ atau dimana saja.
3. Jendela ini disebut disebut sebagai Command Window. Dari jendela ini kita dapat memasukkan perintah Matlab. Disamping itu kita juga dapat menjalankan atau mengeksekusi program yang sudah kita buat di editor window dan disimpan di direktori aktif.
4. Tool yang digunakan untuk mendisplay bantuan pada Matlab.
5. Tool yang dapat digunakan untuk menuju ke Simulink Library Browser.
6. Tool untuk membuka file yang ada di direktori aktiv
7. Tool untuk membuat file baru dengan format M-File.
8. Tool untuk mengatur ukuran jendela.
9. Tool untuk melihat perintah apa saja yang pernah kita jalankan melalui command window. Tool ini diberi nama command history.
10. .Tool untuk mendisplay isi file apa saja yang terdapat di direktori aktif.
11. Tool untuk mendisplay nama variabel, ukuran, bytes dan classnya.
Tool-tool yang sudah disebutkan di atas dapat diatur kemunculannya melalui menu View. Misalnya, kita tidak menginginkan tampilnya jendela command history, maka kita kita harus menghilangkan tanda cek yang ada pada submenu command hstory.
Bab 4
Kasus dan Contoh
4.1 Membuat Grafik Garis
Peranan grafik dalam bidang sains dan teknik adalah sangat penting. Grafik dapat digunakan untuk menampilkan hasil suatu hasil penelitian maupun observasi lapangan. Dengan menampilkan dalam sebuah grafik, pembaca akan dengan mudah memahami atau masalah tertentu. Dapat dibayangkan, misalnya kita memiliki data penelitan sebanyak 10.000 titik data dan semua data disajikan dalam bentuk tabel, sudah tentu kita akan pusing dibuatnya. Lain halnya, jika data tersebut disajikan dalam bentuk grafik, maka dengan mudah kita dapat memahami hasil penelitian tersebut.
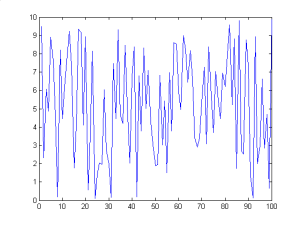
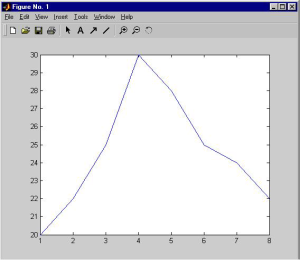
Untuk membuat sebuah grafik garis, fungsi yang kita gunakan adalah plot. Fungsi ini memiliki bentuk berbeda tergantung pada argumen input yang kita berikan. Sebagai contoh, misalnya kita memiliki data dalam bentuk array dan kita simpan dalam vektor y, maka plot(y) akan ditampilkan grafik elemen-elemen y terhadap indeks elemen-elemen tersebut. Sedangkan, jika kita menentukan dua argumen x dan y maka plot(x,y) akan ditampilkan grafik y versus x. contoh
y=10*rand(100,1);
plot(y)
Jika kita memiliki dua buah argumen x dan y, dimana 0≤ x ≥ 10 dan y = cos ( x ) maka grafik y vs x
x=0:pi/200:10*pi;
y=cos(x);
plot(x,y)
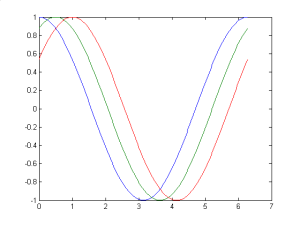
Kita juga dapat membuat beberapa grafik dalam satu frame. Matlab secara otomatis akan membedakan grafik-grafik tersebut dengan warna yang berbeda-beda. Plot tiga grafik dalam satu frame
x=linspace(0,2*pi,200);
y1=cos(x);
y2=cos(x-0.5);
y3=cos(x-1.0);
plot(x,y1,x,y2,x,y3)
4.1.1 Warna, Jenis Garis dan Penanda
Fungsi plot dapat menerima argumen bewujud karakter maupun string yang menyatakan warna, jenis garis dan penanda. Secara umum, bentuk umum
plot(x,y,’JenisGaris_Penanda_Warna’)
rgumen JenisGaris_Penanda_Warna berbentuk string dan diapit oleh tanda petik tunggal.
1. Jenis garis dapat berupa garis putus-putus (dash), titik-tiitk (dot) dan lain-lain.
2. Penanda dapat berupa tanda bintang (*), kotak (square), bulatan (o), diamond, tanda silang (x) dan lain-lain.
3. Warna dapat berupa merah (r), kuning (y), hijau (g), cian (C), hitam (b) dan lain-lain
Sebagai contoh perintah plot(x,y,’-squarer’) akan menampilkan grafik vs x dengan jenis grafik dash (-), penanda kotak (square) dan warna merah.
x=linspace(0,2*pi,200);
y=cos(x);
plot(x,y,’-squarer’)
4.1.2 Plot Grafik untuk Data Berbentuk Matriks
Ketika kita memanggil perintah plot untuk mengeplot grafik data bentuk vektor atau array, maka hasilnya dapat kita lihat seperti contoh-contoh di atas. Nah, bagaimana jika data yang kita miliki berbentuk matriks. Untuk memecahkan masalah ini, marilah kita ingat kembali bahwa vektor memiliki ukuran 1 × m atau m × 1 Perintah plot(y) akan menampilkan setiap elemen dalam kolom atau baris y terhadap indeks elemen vektor tersebut. Demikian pula, perintah plot untuk data Y yang berbentuk matriks akan menampilkan elemen pada setiap kolom atau baris matriks terhadap indeks elemen. Jadi seandainya kita memiliki Y berukuran 10 × 10 , maka kita memiliki 10 (sepuluh) grafik. Sebagai contoh, fungsi peaks merupakan fungsi dua variabel yang menghasilkan matriks 2 dimensi dengan ukuran 49 x 49.
y=peaks;
plot(y)
Jika kita perhatikan, grafik yang terbentuk terdiri atas 49 buah dengan warna berbeda-beda. Secara umum, jika perintah plot digunakan untuk mengeplot grafik fungsi dengan dua argumen dimana data yang terbentuk berupa matriks 2 dimensi, maka
• jika y adalah matriks dan x berupa vektor, maka perintah plot (x,y) akan menampilkan grafik elemen pada kolom/baris matriks y terhadap elemen vektor x.
• jika x adalah matriks dan y berupa vektor, maka plot(x,y) akan menampilkan grafik elemen matriks pada tiap-tiap kolom/baris matriks x terhadap elemen vektor y. Contoh,
x=1:length(peaks);
plot(peaks,x)
4.1.3 Memberikan Label, Legend dan Judul Grafik
Pemberian label pada sumbu-sumbu grafik sangat penting untuk memudahkan pemahaman terhadap makna grafik itu sendiri. Perintah yang digunakan untuk tujuan tersebut antara lain
• xlabel : untuk memberikan label pada sumbu x
• ylabel : untuk memberikan label pada sumbu y
• zlabel : untuk memberikan label pada sumbu z
• tittle : memberikan judul garfik
• legend : untuk memberikan keterangan grafik untuk lebih mudahnya perhatikan contoh di bawah ini,
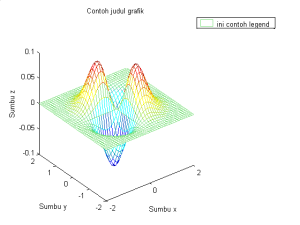
clear; close all;
x=-2:0.1:2;
y=-2:0.1:2;
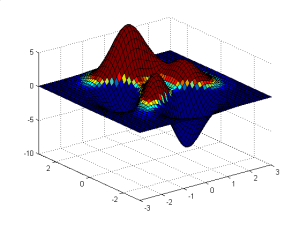
[X,Y]=meshgrid(x,y);
f=-X.*Y.*exp(-2*(X.^2+Y.^2));
mesh(X,Y,f);
xlabel(‘Sumbu x’);
ylabel(‘Sumbu y’);
zlabel(‘Sumbu z’);
title(‘Contoh judul grafik’);
legend(‘ini contoh legend’
4.2 Membuat Plot 3 Dimensi
Apabila kita memiliki dua buah fungsi dengan argumen sama, maka kita dapat menampilkan grafik 3D dari data tersebut. Demikian pula jika kita memiliki 3 buah vektor dengan ukuran sama, maka kita juga dapat menampilkannya menjadi grafik 3D. Contoh
t=-2*pi:pi/200:2*pi;
x=sin(t);
y=cos(t);
plot3(x,y,t);grid
4.2.1 Grafik dengan mesh, surf dan pcolor
sintak untuk plot grafik dengan mesh adalah sebagai berikut,
mesh(X,Y,Z)
mesh(Z)
mesh(…,C)
mesh(…,’PropertyName’,PropertyValue,…)
meshc(…)
meshz(…)
h = mesh(…)
h = meshc(…)
h = meshz(…)
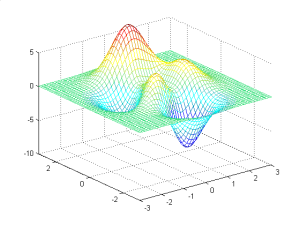
x=-3:.125:3;
y=-3:.125:3;
[X,Y] = meshgrid(x,y);
Z = peaks(X,Y);
mesh(X,Y,Z);
axis([-3 3 -3 3 -10 5])
4.3 Studi Kasus
Buatlah program MATLAB untuk menghitung kecepatan suara.
• Buatlah program MATLAB untuk membuat ping (pulsa yang dipancarkan oleh sensor akustik). Diketahui envelope ping 0.5 (1 – cos(2 π x t /tp) dan carrier sin(2π Cf t) atau cos (2π Cf t). lama pulsa (tp) = 1 detik, carrier frequency (Cf) = 10 Hz, sampling frequency (Sf) = 100 Hz.
• Buatlah program MATLAB untuk menampilkan spectrum gelombang akustik dengan sampling interval (t0) = 0.01, jumlah sampling (Ns) = 128. Cf = 10; Vektor frekuensi dengan Ns element diberikan dengan persamaan x=0.5 (1 – cos(2 π x t /tp) sin(2π Cf t).
Untuk memplot 3 dimensi, anda harus membuat grid tiap titik dalam domain x-y ; Matlab command meshgrid :
x=a:dc:b;
y=c:dy:d;
[X,Y]=meshgrid(x,y);
Perintah terakhir menciptakan 2 matriks X dan Y dengan panjang (y) dan panjang (x) (baris dengan kolom). Elemen tiap elemen merupakan pasangan matriks.
x=[1 2 3];
y=[4 5 6 7];
[X,Y]=meshgrid(x,y)
X = 1 2 3
1 2 3
1 2 3
1 2 3
Y =
4 4 4
5 5 5
6 6 6
7 7 7
X meningkat sepanjang kolom dari kiri ke kanan dalam variable x, Y meningkat dari kiri ke kanan pada baris pada variable y. Jika fungsi dihitung dengan grid, katakan z=f(X,Y), maka perintahnya :
plot3(X,Y,z)
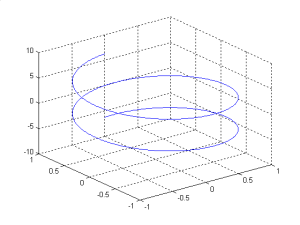
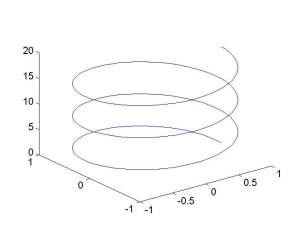
membentuk plot linear seperti perintah plot 2 dimensi. Perintah plot3 sangat berguna dalam kurva ruang (space). Sebagai contoh helix diplot dengan perintah
t=0:pi/30:6*pi;
plot3(cos(t),sin(t),t)
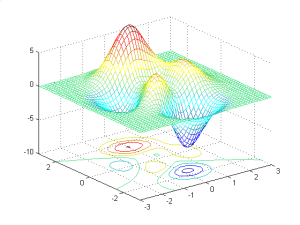
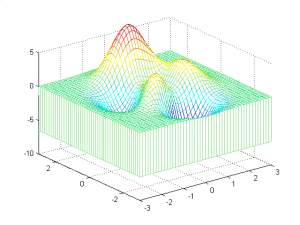
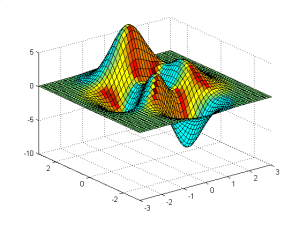
4.3.1 Plot Permukaan (Surface Plots)
Matlab menyediakan 2 perintah untuk plotting surfaces: mesh dan surf. Mesh menggunakan 3-d data dan menciptakan kaitan (wire mesh) melalui tiap titik. surf menciptakan mesh plot dengan ruang diantara garis (lines), mengisi warna menggunakan data z. Ini contohnya :
x=0:pi/20:pi;
y=x;
[X,Y]=meshgrid(x,y);
f=inline(‘sin(2*x).*cos(3/2*y)’,’x’,’y’)
f =
Inline function:
f(x,y) = sin(2*x).*cos(3/2*y)
%Note the function is vectorized
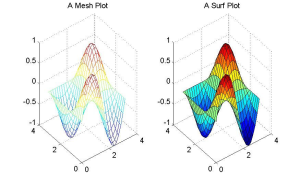
subplot(1,2,1),
mesh(X,Y,f(X,Y))
title(‘A Mesh Plot’)
subplot(1,2,2),
surf(X,Y,f(X,Y))
title(‘A Surf Plot’)
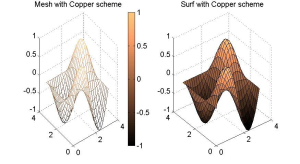
4.3.2 Colormap.
Skema warna untuk suface plots dapat dengan mudah diganti. Beberapa diantara color maps: hot, cool, gray, copper, summer, winter,bone. Menggunakan contoh di atas
>>colormap(whatever you choose)
>colorbar
Color bar meminta Matlab membuat kisaran ‘copper’ dengan nilai fungsi numeric
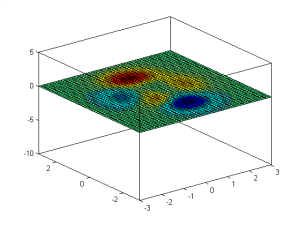
4.3.3 Plot Kontur (Contour Plots)
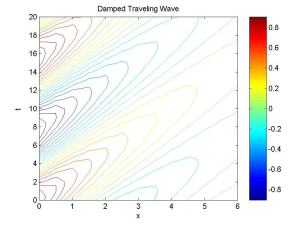
Diberikan data mesh, plot kontur dapat di bangkitkan dengan perintah contour. Sebagai contoh:
x=0:0.5:6;
t=0:0.5:20;
[X,T]=meshgrid(x,t);
g=inline(‘cos(x-0.4*y).*exp(-0.4*x)’,’x’,’y’)
g =
Inline function:
g(x,y) = cos(x-0.4*y).*exp(-0.4*x)
contour(X,T,g(X,T))
colorbar
title(‘Damped Traveling Wave’)
xlabel(‘x’)
ylabel(‘t’)
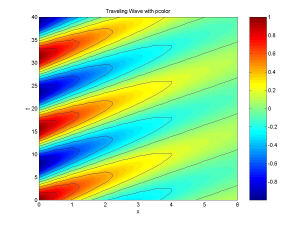
Akhirnya, kombinasi dari patch shading dan contour dapat dilakukan dengan pcolor.
x=0:0.5:6;
t=0:0.5:40;
[X,T]=meshgrid(x,t);
pcolor(X,T,g(X,T))
shading interp
hold on
contour(X,T,g(X,T),’k’)
% ‘k’ membuat garis kontur menjadi hitam
colorbar
title(‘Traveling Wave with pcolor’)
xlabel(‘x’)
ylabel(‘t’)
Bab 5
Penutup
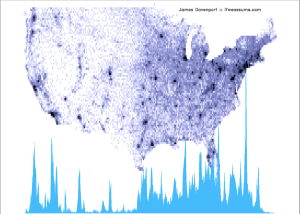
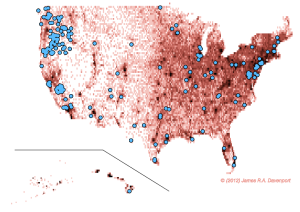
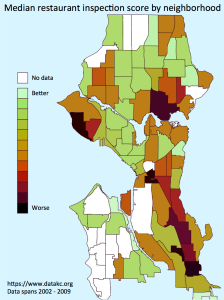
Cubehelix diciptakan untuk membantu banyak sekali bidang, misalnya pada bidang kesehatan cubehelix digunakan untuk membantu orang-orang yang mengidap buta warna, dalam bidang kenegaraan cubehelix digunakan untuk pemetaan kependudukan negara dengan cara menstatistikan bagian-bagian wilayah, dan pada bidang geografis digunakan untuk menentukan kontur-kontur seperti pegunungan, tanah dan lain-lain. Cubehelix di ciptakan dengan berbagai kegunanannya di berbagai bidang dengan menggunakan degradasi warna yang ada di dalamnya.
CubeHelix adalah skema warna yang jenuh yang diperoleh dari warna hitam dan putih . Itu tidak selalu dari warna yang palet dan paling artistik, tetapi cubehelix memiliki keuntungan untuk menjadi lebih mudah melihat bagi orang-orang dengan buta warna . Dengan mengubah berbagai pengaturan , banyak variasi pada ” CubeHelix ” skema yang mungkin terjadi .
Cubehelix adalah skema warna yang digunakan untuk menampilkan gambar Intensitas Astronomi. Skema ini digunakan untuk meningkat kontras cahaya saat greyscale dicetak dalam dua buah warna yaitu hitam dan putih. Cubehelix sendiri tidak memiliki persepsi mendasar mengenai peningkatan kecerahan warna yang digunakan, misalnya warna merah untuk nilai data yang tinggi, dan untuk nilai data menengah digunakan warna kuning atau hijau, untuk mengganti cahaya terang dari warna merah. Untuk mengevaluasi fungsi helix, helix bergerak melalui pemodelan warna yaitu RGB “kubus”, mulai dari hitam (0,0,0) dan berakhir pada warna putih (1,1,1). Poin merata pada helix dalam kubus dikembalikan sebagai warna RGB, Ini memberikan pallet warna yang intensitasnya meningkat secara monoton, yang merupakan pentransfer yang baik untuk menampilkan grayscale atau cetakan. Serta dapat memiliki keuntungan bagi penderita warna blindeness(buta warna). Banyaknya skema warna yang digunakan untuk menampilkan gambar intensitas astronomi tidak memiliki peningkatan yang mendasari terkait persepsi kecerahan warna yang digunakan. Warna adalah properti visual yang sering semua orang gunakan dalam suatu visualisasi tanpa mereka sadari hal itu. Contohnya pada variasi color map pelangi sangat populer, namun terkadang dapat bermasalah dan menyesatkan. Peta warna pelangi tersebut didasarkan pada warna dalam spektrum cahaya, kadangkala peta warna dalam urutan benar, dan kadangkala juga peta warna dalam urutan yang salah. Kecepatan warna pelangi itu merupakan salah satu yang akan menjadi masalah. Bahkan jika warna tersebut digunakan secara konsisten, tak seorang pun akan tahu urutan yang tepat. Sehingga Nama-nama warna mempengaruhi persepsi kita tentang warna.
Software yang di gunakan biasanya berbentuk scientific plotting. Sebuah teknik grafis untuk mewakili satu set data, biasanya sebagai grafik yang menunjukkan hubungan antara dua variabel atau lebih. Plot dapat di gambar dengan tangan atau oleh plotter mekanik atau elektronik.
Matlab ialah suatu perangkat yang dibuat oleh Math Work Inc., digunakan untuk analisis tematika, rancangan kendali, identifikasi sistem dan grafik.
MATLAB (Matrix Laboratory) adalah sebuah program untuk analisis dan komputasi numerik dan merupakan suatu bahasa pemrograman matematika lanjutan yang dibentuk dengan dasar pemikiran menggunakan sifat dan bentuk matriks. Pada awalnya, program ini merupakan interface untuk koleksi rutin-rutin numerik dari proyek LINPACK dan EISPACK, dan dikembangkan menggunakan bahasa FORTRAN namun sekarang merupakan produk komersial dari perusahaan Mathworks, Inc. yang dalam perkembangan selanjutnya dikembangkan menggunakan bahasa C++ dan assembler (utamanya untuk fungsi-fungsi dasar MATLAB). MATLAB telah berkembang menjadi sebuah environment pemrograman yang canggih yang berisi fungsi-fungsi built-in untuk melakukan tugas pengolahan sinyal, aljabar linier dan kalkulasi matematis lainnya. MATLAB juga berisi toolbox yang berisi fungsi-fungsi tambahan untuk aplikasi khusus . MATLAB bersifat extensible , dalam arti bahwa seorang pengguna dapat menulis fungsi baru untuk ditambahkan pada library ketika fungsi-fungsi built-in yang tersedia tidak dapat melakukan tugas tertentu. MATLAB (Matrix Laboratory) yang merupakan bahasa pemrograman tingkat tinggi berbasis pada matriks sering digunakan untuk teknik komputasi numerik, yang digunakan untuk menyelesaikan masalah-masalah yang melibatkan operasi matematika elemen, matrik, optimasi, aproksimasi dll.
5.1 Daftar Pustaka
Jim, 2014, Cubehelix Colormap for Python
http://www.ifweassume.com/2014/04/cubehelix-colormap-for-python.html diakses tanggal 19 Januari 2016
Andry Pujiriyanto ,2008, Cepat Mahir Matlab
https://basayevsmile.files.wordpress.com/2008/09/bab-6-visualisasi-data1.pdf diakses tanggal 19 Januari 2016
Michael Wong, 2012, PENGENALAN MATLAB PADA SISTEM KONTROL
https://wongmichael.wordpress.com/2012/10/21/178/ diakses tanggal 19 Januari 2016
AGUNG SATRIA, 2014, Matlab Toolbox
http://www.academia.edu/5654470/Jobsheet_1_-_Matlab_Toolbox diakses tanggal 19 Januari 2016
Jim, 2013, Cubehelix, or How I Learned to Love Black & White Printers
http://www.ifweassume.com/2013/05/cubehelix-or-how-i-learned-to-love.html?m=1 diakses tanggal 19 Januari 2016
stanford.edu, 2014, Choosing color palettes
https://stanford.edu/~mwaskom/software/seaborn/tutorial/color_palettes.html diakses tanggal 19 Januari 2016
Jim, 2013, cubehelix now for tableau
http://www.ifweassume.com/2013/08/cubehelix-now-for-tableau.html diakses tanggal 19 Januari 2016
grabcad.com, 2015, How to create a cube helix
https://grabcad.com/questions/how-to-create-a-cube-helix diakses tanggal 19 Januari 2016





Tidak ada komentar:
Posting Komentar